Question

You run out of gas in your 1600kg car. You and your friend are capable of producing 300N and 250N of force respectively. How much does the car weight ? (Hint: weight and mass are not the same thing) you and your friend both push the car for 20m, how much work did you collectively perform? After 20m, your friend stops pushing. You push the car another 10m, how much work did you perform in this 10m ? If it took 100s to push the car the first 20m, how much power did you and your friend generate ?First question- 1600 N, 15680N, 16000 N, 1600KgSecond questions- 5000J, 6000J, 11000J, 1000J3rd Question- 5500J, 9000J, 3000J, 2500J4th Question-50W, 60W, 110W, 10W

Answer 1

Given that the mass of the car is m = 1600 kg

(a) We have to find the weight of the car.

The weight of the car is given by the formula

`W=mg`

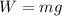
Here, g =9.8 m/s^2 is the acceleration due to gravity.

Substituting the values, the weight of the car will be

`\begin{gathered} W=1600*9.8 \\ =15680\text{ N} \end{gathered}`

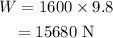
The correct option is the second option: 15680 N

(b) Given that the two push forces are F1 = 300 N and F2 = 250 N

The distance traveled by car due to pushing is d = 20 m

The total force will be

`\begin{gathered} F=F1+F2 \\ =300+250 \\ =\text{ 550 N} \end{gathered}`

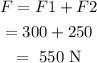
We have to find the total work done.

The work done can be calculated by the formula

`W=F* d`

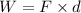
Substituting the values, the work done will be

`\begin{gathered} W=550*20 \\ =11000\text{ J} \end{gathered}`

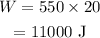
The correct option is the third option: 11000 J

(c) The force applied by you is F1 = 300 N.

The distance covered is d' = 10 m.

We have to find the work done.

The work done will be

`\begin{gathered} W1\text{ = F1}* d^(\prime) \\ =300*10 \\ =3000\text{ J} \end{gathered}`

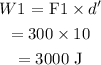
The correct option is the third option: 3000 J

(d) The work done to push 20 m is W = 11000 J

The time taken is t = 100 s

We have to find the power generated.

The power can be calculated by the formula

`P=(W)/(t)`

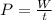
Substituting the values, the power will be

`\begin{gathered} P=(11000)/(100) \\ =110\text{ W} \end{gathered}`

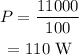
Thus, the correct option is third option: 110 W