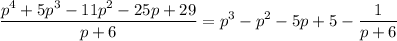Question

Divide the polynomial using synthetic division(p^4 +5p^3 - 11p^2 – 25p +29) ÷ (p+6)

Answer 1

We are required to evaluate using Synthetic division:

`\left(p^4+5p^3-11p^2-25p+29\right)/(p+6)`

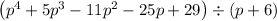
To do this, we follow these steps:

Step 1: Set the denominator equal to zero to find the number to put in the division box. Next, make sure the numerator is written in descending order.

p+6=0

Therefore: p =-6

Step 2: Bring the leading coefficient down as follows.

Step 3: Multiply the number in the division box (-6) with the number you brought down (1) and put the result in the next column. Add the two numbers together and write the result in the bottom of the row.

Step 4: Multiply the number in the division box(-6) with the number you brought down (-1) and put the result in the next column.

Step 5: We repeat the same process until the last digit.

Step 6: The last digit is the remainder. Therefore we write our result taking note that the power of p will start from 3 which is one less the original function.

:

`\begin{gathered} (p^4+5p^3-11p^2-25p+29)/(p+6)=p^3-p^2-5p+5-(1)/(p+6) \\ \end{gathered}`