Step-by-step explanation
Given that each ladder is 3.5 meters away from the base of the building, we are asked to find the height of the building. This can be seen below,
Number 1:
The height of ladder A is 5.5 meters. We can then use the Pythagoras theorem to find the height of the window.
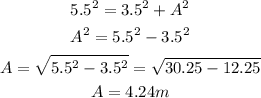
Answer: Height of window A =4.24m
Number 2
The height of ladder B is 8.8 meters. We can then use the Pythagoras theorem to find the height of the window.
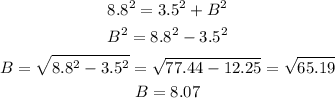
Answer: Height of window B =8.07m
Number 3
The height of ladder B is 9.3 meters. We can then use the Pythagoras theorem to find the height of the window.
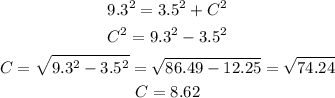
Answer: Height of window C =8.62m
Number 4
The height of ladder B is 7.9 meters. We can then use the Pythagoras theorem to find the height of the window.
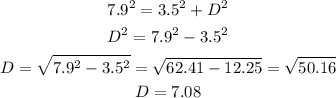
Answer: Height of window D = 7.08m