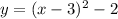The given vertex is (3,-2), so we can use the standard form to find the equation

Assuming that a = 1, let's replace the given values of the vertex
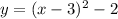
However, a must be negative so the parabola has no x-intercepts.
Hence, the answer to (a) is

The solutions of this equation above are not real numbers because there aren't x-intercepts. In other words, the discriminant is negative.
To answer part b, we have to say that a is positive, so the equation is