ANSWER
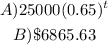
Step-by-step explanation
The general form of an exponential loss is given by:
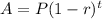
P = initial value of the car.
r = rate of decrease
t = amount of time (in years)
18. Substitute the given values into the equation to find the model that represents the value after t years:
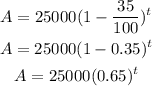
That is the model that represents the value after t years.
19. To find the value of the vehicle at the end of the 3rd year, we have to solve for A when t is 3:
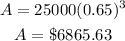
That is the answer.