Given the points:
(-9, 10) and (-1, 12)
Let's find the equation of the circle using the points which are the endpoints of the diameter.
Apply the general equation for a circle:

Where:
• (h, k) is the center
,
• r is the radius of the circle.
Let's first find the diameter of the circle using the distance between points formula:
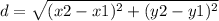
Where:
(x1, y1) ==> (-9, 10)
(x2, y2) ==> (-1, 12)
Hence, we have:

The diameter of the circle is 8.2 units.
To find the radius, we have:
radius = diameter/2 = 8.2/2 = 4.1 units
The radius of the circle is 4.1 units.
Now, let's find the center of the circle.
To find the center of the circle, apply the midpoint formula:

Thus, we have:

The center of the circle is (-5, 11).
Therefore, the equation of the circle with the points is:
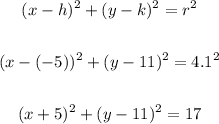
ANSWER:
