Given:
The length of a rectangle is 8 inches more than its width.
The area of the rectangle is equal to 3 inches less than 3 times the perimeter.
Find-: Length and width of the rectangle.
Sol-:
The perimeter of a rectangle is:

Let width = b
length =l
If the length of a rectangle is 8 inches more than its width then:

The area of a rectangle is:

If the area of the rectangle is equal to 3 inches less than 3 times the perimeter.
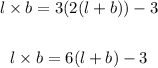
Put the value of "l"
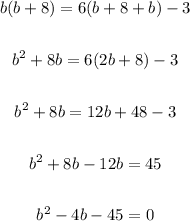
Solve for "b" is:
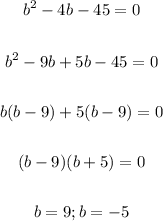
"b" is the width of a rectangle so the value of "b" is a non-negative value.
So value of "b" is 9.
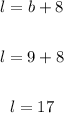
Length of rectangle is 17 and width is 9.