Given:
7, 7, 6, 10, 10
To find the standard deviation assuming that the scores constitute an entire population, we first note the formula:
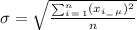
where:
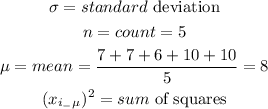
Next,we get the sum of squares as shown below:
Then, we solve for the standard deviation:
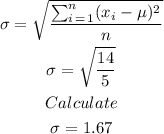
Therefore, the answer is: 1.67