Question

Which equation has exactly one solution?A 5(y - 3) = 2y + 3yB 5(y - 3) = 2y + 3© 5(y - 3) – 3y = 2yD5(y - 3) + 15 = 2y + 3y

Answer 1

We want to know which equation has exactly one solution

Let's look at them one after the other

A,. we have

`\begin{gathered} 5(y-3)=2y+3y \\ 5y-15=5y \\ collect\text{ like terms } \\ 5y-5y=15 \\ We\text{ can't have 5y subtracting 5y} \end{gathered}`

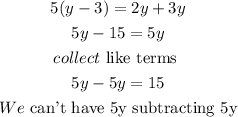
So this is infinitely many solutions

B.,

`\begin{gathered} 5(y-3)=2y+3 \\ 5y-15=2y+3 \\ collect\text{ like terms } \\ 5y-2y=3+15 \\ 3y=18 \\ y=(18)/(3) \\ y=6 \end{gathered}`

This has exactly one solution, which is y = 6.

But let's check for C and D

C,.

`\begin{gathered} 5(y-3)-3y=2y \\ 5y-15-3y=2y \\ collecting\text{ like terms } \\ 5y-3y-2y=15 \\ 5y-5y=15 \\ \end{gathered}`

This is also infinitely many solutions like A

D,.

`\begin{gathered} 5(y-3)+15=2y+3y \\ 5y-15+15=5y \\ 5y+0=5y \\ 5y-5y=0 \end{gathered}`

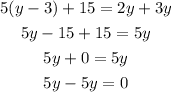
This also has infinitely many solutions like A and C

Hence the answer is option B