Question

Find the solution of this system of equations8x+4y=07x+8y=9

Answer 1

We are given the following two equations

`\begin{gathered} 8x+4y=0\quad eq.1 \\ 7x+8y=9​\quad eq.2 \end{gathered}`

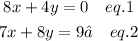
Let us solve these equations using the substitution method.

Separate out one variable from eq. 1

`\begin{gathered} 8x+4y=0 \\ 4y=-8x \\ y=-(8x)/(4) \\ y=-2x\quad eq.1 \end{gathered}`

Now substitute this value of y into the eq.2

`\begin{gathered} 7x+8y=9 \\ 7x+8(-2x)=9 \\ 7x-16x=9 \\ -9x=9 \\ x=(9)/(-9) \\ x=-1 \end{gathered}`

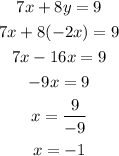
So, we got the value of x and we can substitute this value into eq.1 to find the value of y.

`\begin{gathered} y=-2x \\ y=-2(-1) \\ y=2 \end{gathered}`

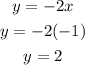
Therefore, the solution of this system of equations is

x = -1 and y = 2