Question

Solving a value mixture problem using a system of linear equations

Answer 1

We must solve this problem using a system of linear equations

We know that the Martines family has 20 liters per hour sprinklers and the Hall family has 30 liters per hour sprinklers, used together for 35 hours they consume 850 liters of water

We can do two equations, one for water expenditure as a function of time and one for time

`30x+20y=850`

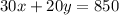
"x" is the number of hours the sprinkler is used from the Hall family's sprinklers and "y" is the number of hours the sprinkler is used from the Martinez family's sprinkler

`x+y=35`

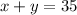
Now we can clear x and leave everything in terms of "y" to solve the first equation and subsequently the times of both families

`x=35-y`
`\begin{gathered} 30\cdot(35-y)+20y=850 \\ 1050-30y+20y=850 \\ -10y=-200 \\ 10y=200 \\ y=(200)/(10)=20 \end{gathered}`

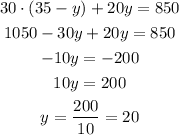
Now we can solve "x"

`x=35-20=15`

If we replace in the equation these values for "x" and for "y" we should get 850

`\begin{gathered} 15\cdot30+20\cdot20=850 \\ 450+400=850 \end{gathered}`

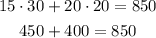
In conclusion, the Hall family's sprinkler: 15 hours and the Martinez family's sprinkler: 20 hours