Given,
The radius of the earth, r=6.371×10³ km=6.371×10⁶ m
The gravitational strength at the surface of the earth is given by,

Where G is the gravitational constant and M is the mass of the earth.
Thus the gravitational field strength at a height h, where the gravitational field strength would be two-third of its values at the surface is,
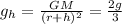
Thus,
![\begin{gathered} (GM)/((r+h)^2)=(2GM)/(3r^2) \\ \Rightarrow(3)/(2)r^2=(r+h)^2 \\ \Rightarrow\sqrt[]{(3)/(2)}r=r+h \\ \Rightarrow h=r(\sqrt[]{(3)/(2)}-1) \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/t2x3v57nwqe30u962ks3op4mqehnbi4v72.png)
On substituting the value of r,
![\begin{gathered} h=6.371*10^6(\sqrt[]{(3)/(2)}-1) \\ =6.371*10^6(0.225) \\ =1.433*10^6\text{ m} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/1elbvpcpqu9rndi59ziz4yqi6vakre43or.png)
Thus the earth's gravitational field strength would be two-thirds of its value at the surface at a height of 1.433×10⁶ m above the surface.
The height at which the gravitational field strength would be one-fourth its value at the surface is given by,
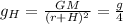
Thus,
![\begin{gathered} (GM)/((r+H)^2)=(GM)/(4r^2) \\ 4r^2=(r+H)^2 \\ \sqrt[]{4}r=r+H \\ \Rightarrow H=2r-r=r \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/wymx3qk0upcbkpij9fztwzop67n8be89kb.png)
Therefore,

Thus the earth's gravitational field strength would be one-fourth of its value at the surface at a height of 6.371×10⁶ m above the surface.