Given that the ride-sharing company has computed its mean fare to be $33.00, with a standard deviation of $4.10, this implies that
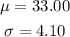
The z score value is expressed as

A) Approximately 68% of the company's rides have fares between . . .
From the normal distribution table,
this implies that the z score value is
![undefined]()