Question

Find the exact value of each of the remaining trig functions of θa. sinθ= 12/13 , θ in quadrant II

Answer 1

We have an angle θ in the II quadrant for which sin(θ) = 12/13.

We have to find the cosine of θ.

We can start by drawing a possible angle:

We can relate the cosine and sine of an angle with the identity:

`\sin ^2(\theta)+\cos ^2(\theta)=1`

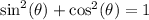
We then can calculate cos(θ) as:

`\begin{gathered} \cos ^2(\theta)=1-\sin ^2(\theta) \\ \cos ^2(\theta)=1-((12)/(13))^2 \\ \cos ^2(\theta)=1-(144)/(169) \\ \cos ^2(\theta)=(169-144)/(169) \\ \cos ^2(\theta)=(25)/(169) \\ \cos ^2(\theta)=(5^2)/(13^2) \\ \cos ^2(\theta)=((5)/(13))^2 \\ (\pi)/(2)<\theta<\pi\Rightarrow\cos (\theta)<0\Rightarrow\cos (\theta)=-(5)/(13) \end{gathered}`

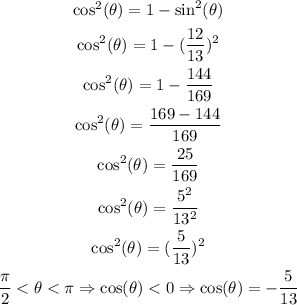
NOTE: the last step is because we know that the angle θ is in the second quadrant. Therefore, the cosine of θ is negative (see picture above). The identity is still valid, because the square of (-5/13) is still 25/169.

Now, we can calculate the tangent of θ as:

`\tan (\theta)=(\sin (\theta))/(\cos (\theta))=((12)/(13))/(-(5)/(13))=(12)/(-5)=-(12)/(5)`

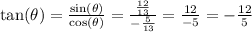
Answer:

cos(θ) = -5/13

tan(θ) = -12/5