Question

A stone is thrown vertically upward from a platform that is 20 feet above ground at a rate of 80 feet per second.

Answer 1

Given that the stone is thrown vertically upwards from a platform that is 20 feet above the ground at a rate of 8 feet per seconds, using a projectile formula:

`\begin{gathered} h=-16t^2+v_0t+h_0\text{ ------ equation 1} \\ where \\ v_0\Rightarrow initial\text{ velocity of the stone} \\ h_0\Rightarrow initial\text{ height of the stone} \end{gathered}`

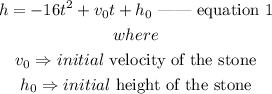
To calculate the maximum height and the time it takes to reach this height,

step 1: Take the derivative of h with respect to t.

Thus,

`\begin{gathered} h^(\prime)=(dh)/(dt)=-32t+v_0 \\ \Rightarrow h^(\prime)=-32t+v_0 \end{gathered}`

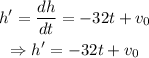
step 2: Determine the critical point of the function (equation 1).

At the critical point, h' equals zero.

Thus,

`\begin{gathered} h^(\prime)=-32t+v_0 \\ where \\ h^(\prime)=0\text{ at the critical point} \\ thus, \\ -32t+v_0=0 \\ where\text{ v}_0=80 \\ thus, \\ -32t+80=0 \\ subtract\text{ 80 from both sides of the equation} \\ -32t+80-80=0-80 \\ \Rightarrow-32t=-80 \\ divide\text{ both sides by the coefficient of t, which is -32} \\ thus, \\ -(32t)/(-32)=-(80)/(-32) \\ \Rightarrow t=2.5\text{ seconds} \end{gathered}`

step 3: Determine the extreme point of the function.

To determine the extreme point of the function, we take the second derivative of the function.

`\begin{gathered} h^(\prime)^(\prime)=(d^2h)/(dt^2)=-32 \\ \end{gathered}`
`\begin{gathered} when\text{ h''>0, we have a minimum point} \\ when\text{ h''<0, we have a maximum point} \end{gathered}`

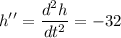
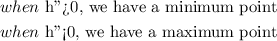
Since, the second derivative obtained is negative (less than zero), we have a maximum point.

Thus, the stone reaches the maximum height after 2.4 seconds.

step 4: Evaluate the maximum height reached by the stone.

To evaluate the maximum height reached by the stone, substitute the value of 2.5 for t in equation 1.

Thus, from equation 1,