Question

4. Sketch the graph of y = (x - 1)*+2 and identify the axis of symmetry.Ox=1X-1x = 2x = -2

Answer 1

The equation:

`y=(x-1)^2+2`

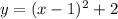
has the form:

`y=(x-h)^2+k`

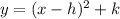
where the point (h, k) is the vertex of the parabola. In this case, the vertex is located at (1, 2).

The axis of symmetry is

x = h

x = 1

To graph the function we need three points. One of them is the vertex. The other two should be at the same distance from the axis of symmetry. Substituting with x = 0 into the equation, we get:

`\begin{gathered} y=(0-1)^2+2 \\ y=1+2 \\ y=3 \end{gathered}`

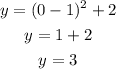
Substituting with x = 2 into the equation, we get:

`\begin{gathered} y=(2-1)^2+2 \\ y=1+2 \\ y=3 \end{gathered}`

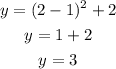
Connecting with a parabola the points (0, 3), (1, 2), and (2, 3) we get: