Question

An object is dropped from a height of 400 feet. Its height, h(t) in feet, after t seconds, is modeled by the equation h(t) = 400 - 16t^2. What is the domain of h(t)?O A. all real numbers greater than 0O B. all real numbers greater than 0 and less than 5O C. all real numbers greater than 0 and less than 16O D. all real numbers greater than 0 and less than or equal to 5O E. all real numbers greater than 0 and less than or equal to 16

Answer 1

The domain of a function is all values that the independent variable can assume.

In this case, the independent variable is the time t.

Since the time can't be negative, we have the condition t > 0.

Also, the height can't be negative as well, so we have:

`\begin{gathered} h(t)\ge0 \\ 400-16t^2\ge0 \\ -16t^2\ge-400 \\ 16t^2\le400 \\ t^2\le(400)/(16) \\ t^2\le25 \\ -5\le t\le5 \end{gathered}`

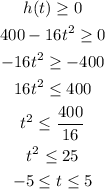
Calculating the intersection of these two conditions, we have that the values of t need to be greater than 0 and less than or equal to 5.

Therefore the correct option is D.