Question

The velocity of a particle movie along the x-axis is v(t) = t^2 - 2t, with t measured in minutes and v(t) measured in feet per minute. To the nearest foot find the total distance traveled by the particle from t = 0 to t = 3 minutes.

Answer 1

zero

Step-by-step explanation

we know that when derivantind the position function respecto to time we got the function for velocity, so we can integrate the given function to obtain the function for velocity

hence

Step 1

a) integrate to find the function for distance travelede

`\begin{gathered} v(t)=t^2-2t \\ integrate \\ \int(t^2-2t)\text{ dt} \\ \int(t^2-2t)\text{ dt=}(t^(2+1))/(2+1)-(2t^(1+1))/(2) \\ \int(t^2-2t)\text{ dt=}(t^3)/(3)-t^2 \end{gathered}`

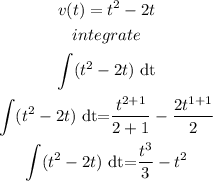
so

`\begin{gathered} d(t)=(t^3)/(3)-t^2+C \\ C=initial\text{ distance , so c=0} \end{gathered}`

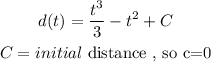
Step 2

now,we have the functio for the distance,

a) evaluate for t=0

`\begin{gathered} d(t)=(t^3)/(3)-t^2 \\ d(0)=(t^(3))/(3)-t^2=(0^3)/(3)-0^2=0-0=0 \\ d(0)=0 \end{gathered}`

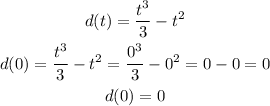
b) evaluate for t=3 minutes

`\begin{gathered} d(t)=(t^3)/(3)-t^2 \\ d(3)=(3^3)/(3)-3^2=(27)/(3)-9=9-0 \\ d(3)=0 \end{gathered}`

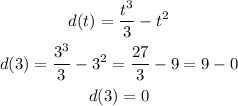
now, find the total distance traveled by the particle from t = 0 to t = 3 minutes., subtract the positions

`distance=\Delta d=0m-0m=0m`

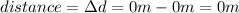
so, the total displacement would be zero,but :

the particle actually travels ,it start in negative direction,and then it moves to positive direction, after 3 minutes the particle is in the same place

so, the answer is zero