First, let's calculate the derivative:
![f^(\prime)(x)=(d)/(dx)(\sin \sqrt[]{x})](https://img.qammunity.org/2023/formulas/mathematics/college/78ne47ippd6ta0ll72o55vf258b9x8oub1.png)
Here we have a compounded function, so we need to apply the chain rule:
![f^(\prime)(x)=\cos \sqrt[]{x}\cdot(d)/(dx)(\sqrt[]{x})](https://img.qammunity.org/2023/formulas/mathematics/college/1xoppfrgtw5pdo0rlz52u8dnisvgit2c2o.png)
Finally, we obtain:
![f^(\prime)(x)=\cos \sqrt[]{x}\cdot(\frac{-1}{2\cdot\sqrt[]{x}})](https://img.qammunity.org/2023/formulas/mathematics/college/dq1dre9zut7wcdziag477cigwyg027oj2n.png)
![f^(\prime)(x)=-\frac{\cos \sqrt[]{x}}{2\cdot\sqrt[]{x}}](https://img.qammunity.org/2023/formulas/mathematics/college/junkkmj3ngi22ar1callb79jx50cn0qhwq.png)
Now, let's establish the relationship:
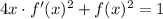
replacing the expressions of the functions:
![4x\cdot(\frac{\cos\sqrt[]{x}}{2\cdot\sqrt[]{x}})^2+\sin ^2\sqrt[]{x}=1](https://img.qammunity.org/2023/formulas/mathematics/college/sdkuce9vg2d1m96drcp655f3pazk37noa9.png)
![4x\cdot\frac{\cos^2\sqrt[]{x}}{2^2\cdot\sqrt[]{x}^2}+\sin ^2\sqrt[]{x}=1](https://img.qammunity.org/2023/formulas/mathematics/college/caxhv5x0ltfnxtscfsqjb549afnepbv4zp.png)
![4x\cdot\frac{\cos^2\sqrt[]{x}}{4x}+\sin ^2\sqrt[]{x}=1](https://img.qammunity.org/2023/formulas/mathematics/college/y7pkabglqclockksntdln87embfp27sm72.png)
We can cancel the terms 4x in the first term of the expression:
![\cos ^2\sqrt[]{x}+\sin ^2\sqrt[]{x}=1](https://img.qammunity.org/2023/formulas/mathematics/college/p5fvtt7lpjskkwdbj4w5c36r3yg1qnbodn.png)
From the Pythagorean identity, we know that the sum of cosine squared, plus sine squared of any angle is always equal to 1:
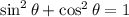
Then, we confirm that the relationship established in 2) is correct:
![\begin{gathered} \cos ^2\sqrt[]{x}+\sin ^2\sqrt[]{x}=1 \\ \\ 1=1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/jytjwx33rx9kymsd9973kifj3ue12x15fa.png)