Step 1
State N(T) and T(t)
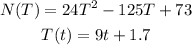
T is the temperature of the food
t is time in hours when the food is outside the refrigerator
Step 2
Find N(T(t))
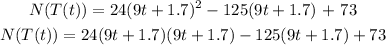
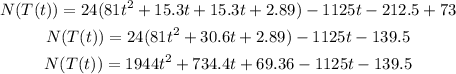
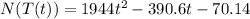
Step 3
Find the time when the bacteria count reaches 24722
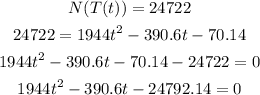
Step 4
Find t using the quadratic formula.
![\begin{gathered} t=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{where} \\ a=1944 \\ b=-390.6 \\ c=-24792.14 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/o5t8zr9u3zbj4x8fe6pphur3s3v6gkthu3.png)
![\begin{gathered} t=\frac{-(-390.6)\pm\sqrt[]{(-390.6)^2-4*1944*-24792.14}}{2*1944} \\ t=\frac{390.6\pm\sqrt[]{152568.36+192783680.6}}{3888} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/nsqixpj2n4zcnu1zuevo3miebtyiaxdd36.png)
![\begin{gathered} t=\frac{390.6\pm\sqrt[]{192936249}}{3888} \\ t=(390.6\pm13890.14935)/(3888) \\ t=(390.6+13890.14935)/(3888)=3.67303224\text{ hrs} \\ or \\ t=(390.6-13890.14935)/(3888)=-3.472106314\text{ hrs} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/pozq3lzckw7ha6l46ntm750wd3mehy4drg.png)
Since time cannot be negative t = 3.67303224 hrs