ANSWER
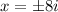
Step-by-step explanation
We want to solve the equation:
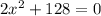
This can be solved using the square root method.
To do this, first, separate the terms in the equation:
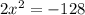
Next, divide both sides by 2:
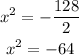
Then, find the square root of both sides of the equation:
![\begin{gathered} \sqrt[]{x^2}=\sqrt[]{-64} \\ x=\sqrt[]{64\cdot-1}=\sqrt[]{64}\cdot\sqrt[]{-1} \\ x=\pm8\cdot i \\ x=\pm8i \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ggn2hhd7n1bc7xre3gizmcya6w4ck8buvy.png)
That is the solution to the equation.