Question

The amount of a radioactive isotope present at time t is given by A(t)=800e−0.02884t grams, where t is the time in years that the isotope decays. The initial amount present is 800 grams. Complete parts (a) through (c)You have to complete a to get b and And complete b to get c. This problem has 3 steps

Answer 1

(a) You know that this function represents the amount of a radioactive isotope present at time "t" (in years):

`A\mleft(t\mright)=800e^(-0.02884t)`

Then, in order to find the number of grams remain after 15 years, you need to set up that:

`t=15`

Now you need to substitute this value into the function and evaluate:

`\begin{gathered} A(15)=800e^((-0.02884)(15)) \\ A(15)\approx519.06 \\ \end{gathered}`

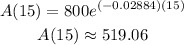
(b