Question

A series RLC circuit has a resistance of 54.33 ohm, a capacitance of 2.56 microF, and an inductance of 172.91 mH. The circuit is connected to a variable-frequency source with a fixed rms output of 54.03 V. The frequency is 60 Hz.• Determine the power factor.

Answer 1

Given:

R = 54.33 Ohm

C = 2.56 micro F

L = 172.91 mH

f = 60 Hz

To find:

The power factor.

Step-by-step explanation:

The inductive reactance can be calculated as:

`X_L=2\pi fL=2\pi*60*172.91*10^(-3)=65.1855\text{ Ohm}`

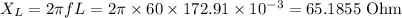
The capacitive reactance can be calculated as:

`X_C=(1)/(2\pi fC)=(1)/(2\pi*60*2.56*10^(-6))=(1)/(9.6509*10^(-4))=1036.172\text{ Ohm}`

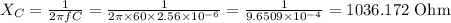
The phase angle is given as:

`\varphi=tan^(-1)((X_L-X_C)/(R))=tan^(-1)((65.1855-1036.172)/(54.06))=-86.81\degree`

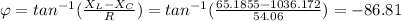
The power factor is given as:

`P.F=cos\varphi=cos(-86.81\degree)=0.0556`

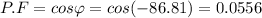
Final answer:

The power factor is 0.0556.