We want to find the oblique asymptote for the following function
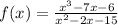
To find the oblique asymptote, we just need to effectuate the division and analyse its behavior as it goes to infinity.
Doing the division, we have
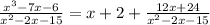
The rational term approaches 0 as the variable approaches infinity.
Thus, the oblique asymptote is y = x + 2