Question

At what rate is his distance increasing from home plate when he is 60 feet from second base

Answer 1

We can start by writing a diagram of the baseball diamond:

We have to calculate the rate of change of y, the distance of the player to the home base, when x, the distance of the player from the first base, is 30 ft (that is 90 ft - 60 ft).

The rate of increase of x is 22 ft/s.

Then, we know that:

`v_x=(dx)/(dt)=22`

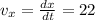
and that, by the chain rule:

`(dy)/(dt)=(dy)/(dx)\cdot(dx)/(dt)`

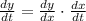
We then have to find dy/dx.

We can relate them using the graph:

Then, using the Pythagorean theorem we can write:

`\begin{gathered} y^2=90^2+x^2 \\ y=\sqrt[]{90^2+x^2} \end{gathered}`

Knowing y = f(x), we can calculate the first derivative as:

`\begin{gathered} (dy)/(dx)=\frac{d(\sqrt[]{90^2+x^2})}{dx} \\ (dy)/(dx)=(1)/(2)\frac{1}{\sqrt[]{90^2+x^2}}\cdot2x \\ (dy)/(dx)=\frac{x}{\sqrt[]{90^2+x^2}} \end{gathered}`

Then, applying the chain rule, we get:

`(dy)/(dt)=(dy)/(dx)\cdot(dx)/(dt)=\frac{x}{\sqrt[]{90^2+x^2}}\cdot22=\frac{22x}{\sqrt[]{90^2+x^2}}`

We can now calculate dy/dt, the rate of change of the distance to the home base, when x = 30 ft as:

`\begin{gathered} (dy)/(dt)=\frac{22x}{\sqrt[]{90^2+x^2}} \\ (dy)/(dt)(30)=\frac{22\cdot30}{\sqrt[]{90^2+30^2}} \\ (dy)/(dt)(30)=\frac{660}{\sqrt[]{8100+900}} \\ (dy)/(dt)(30)=\frac{660}{\sqrt[]{9000}} \\ (dy)/(dt)(30)\approx(660)/(94.868330) \\ (dy)/(dt)(30)\approx6.96 \end{gathered}`

Answer: the rate of change of the distance to the home base when the player is at 60 ft from the second base is 6.96 ft/s.