Question

A plane is traveling with a velocity of 70 miles/hr with a direction angle of 24 degrees. The wind is blowing at 25 miles/hr with a direction angle of 190 degrees. What is the direction angle of planes resultant vector (velocity)? Round your answer to the nearest whole number.

Answer 1

46 miles/hr with a direction angle of 32°

Step-by-step explanation

Given:

• The velocity of the plane, ,v, = 70 mi/h at 24°

,

• The velocity of the wind, ,u, = 25 m/h at 190°

Find:

• The resultant velocity of the plane, ,u, + ,v

First, let's draw each vector,

The resultant is the sum of the two vectors, so first, we have to find the vectors in the form . The components of a vector form a right angle with the vector itself. The x-component is the adjacent side to the direction's angle and the y-component is the opposite side.

For the velocity of the car, we have,

`\vec{v}=<70\cos24\degree,70\sin24\degree>`

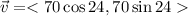
The two components of the wind's velocity are negative because the vector is on the third quadrant. The angle in the triangle is 190 - 180 = 10°,

`\vec{u}=\lt-25\cos10\degree,-25\sin10\degree>`

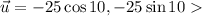
The sum of the two vectors is,

`\vec{v}+\vec{u}=\lt(70\cos24\degree-25\cos10\degree),(70\sin24\degree-25\sin10\degree)>`

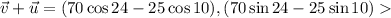
Let's solve this,

`\vec{v}+\vec{u}=\lt39.3280,24.1304>`

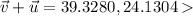
The magnitude of the resultant, by the Pythagorean Theorem, is,

`||\vec{v}+\vec{u}||=√(39.3280^2+24.1304^2)\approx46.1407\approx46\text{ }mi/h`

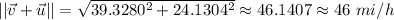
And using the tangent of the direction angle, we can find the direction of the resultant,

`\theta=\tan^(-1)\left((24.1304)/(39.3280)\right)\approx31.5319\degree\approx32\degree`

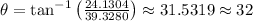
Hence, the resultant is 46 miles/hr with a direction angle of 32°, rounded to the nearest whole number.