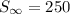Question

If the first 5 terms of an infinite geometric sequence are 100, 60,36, 21.6 , and 12.96, then the sum of all the terms in the sequence is _______.

Answer 1

This is a geometric sequence since there is a common ratio between each term. In this case, multiplying the previous term in the sequence by 3/5 gives the next term. In other words,

`a_n\text{ = }a_1r^(n-1)`

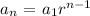
where r = 3/5. Now, The sum of a series S_n is calculated using the formula:

`S_n\text{ = }(a(1-r^n))/(1-r)`

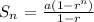
For the sum of an infinite geometric series, as n approaches infinity we have that 1-r^n approaches 1. Thus

`\text{ }(a(1-r^n))/(1-r)`

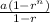
approaches

`\text{ }(a)/(1-r)`

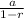
then the sum of an infinite geometric series would be:

`S_(\infty)=(a)/(1-r)_{}`

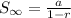
The values a = 100 and r = 3/5 can be put in the previous equation:

`S_(\infty)=(100)/(1-(3)/(5))_{}=\text{ }250`

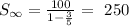
then, the correct answer is:

`S_(\infty)=250`