ANSWER:
0.536 mm/s²
Explanation:
Given:
Solar intensity (I) = 1380 W/m²
Area (A) = 43,318.28 m²
Mass (m) = 743.39 kg
Speed of light (v) = 3*10^8 m/s
We can calculate the pressure using the following formula:
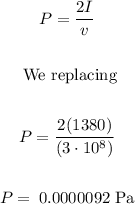
We can determine the acceleration knowing the following:

The acceleration is equal to 0.536 mm/s²