1 Answer

Tomak · Answer 1 · 2023-07-12T01:28:02+0000

Question:

Solution:

a) Consider the following equation:

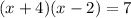
applying the distributive property, we get:

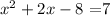
$x^2+2x-8\text{ =}7$

now, putting all terms on one side of the equation, we get:

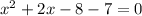
this is equivalent to:

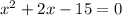
Factoring this expression, we get:

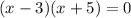
according to the equation, we can conclude that the solutions for the given equation are:

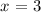
$x\text{ = 3}$

and

$x=\text{ }-5$

b) Consider the following equation:

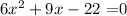
$6x^2+9x-22\text{ =0}$

applying the quadratic formula:

$\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}$

where

a = 6,

b = 9

and

c = -22,

we obtain that the solutions of the given equations are:

$x\text{ =}\frac{-9+\sqrt[]{609}}{12}=\text{ 1.3}0$

and

$x\text{ =}\frac{-9-\sqrt[]{609}}{12}=\text{ -2.8}0$

Please log in or register to add a comment.