Notice the following pattern
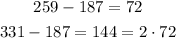
This reflects a linear behavior; therefore, we can find the equation of the function represented by the table using two points on it and the equation below
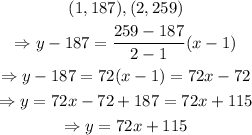
Set h=x and c=y; thus, the answer to part A is
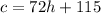
Set h=6 and solve for c, as shown below.
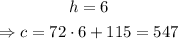
The answers to part A are c=72h+115, and the cost of 6 hours of work is $547
Part B)
According to the problem, if c is the total cost and h is the number of hours; the equation that represents the function is
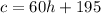
Setting h=6 and solving for c,
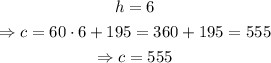
The answers to part B are c=60h+195, and the cost for 6 hours of work is $555.
Part C)
As we found in parts A and B, the least expensive carpenter for 6 hours of work is Carpenter L; however, this is the case if only 6 hours of work are required; if that changes, it could alter the answer.