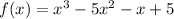Question

Hello can you help me simplify my answer I have the answer but can’t simplify it

Answer 1

The Solution:

Given that the zeros of a polynomial function of degree 3, are:

`-1,1,5`

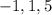
We are required to form the polynomial function of degree 3 with a leading coefficient of 1.

Step 1:

`\begin{gathered} x=-1 \\ x=1 \\ x=5 \\ \text{This means that:} \\ x+1=0 \\ x-1=0 \\ x-5=0 \end{gathered}`

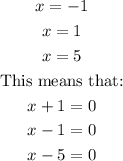
Step 2:

The required polynomial will be

`(x+1)(x-1)(x-5)=0`

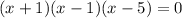
Clearing the brackets, we get

`\begin{gathered} \lbrack(x+1)(x-1)\rbrack(x-5)=0_{} \\ \lbrack x(x-1)+1(x-1)\rbrack(x-5)=0 \\ (x^2-x+x-1)(x-5)=0_{} \\ (x^2-1)(x-5)=0_{} \end{gathered}`
`\begin{gathered} x^2(x-5)-1(x-5)=0 \\ x^3-5x^2-x+5=0 \end{gathered}`

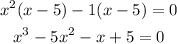
Therefore, the required polynomial is

`f(x)=x^3-5x^2-x+5`