We are given the points (2,-7) and (-3,3) to find the equation of the line that passes through them. Recall that the slope-intercept form of the line equation is of the form
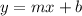
where m is the slope and b is the y-intercept.
We can calculate the slope m as follows: Given points (a,b) and (c,d) the slope of theline that passes through them is given by the formula
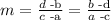
In our case we have a=2, b=-7, c=-3 and d=3 So we get
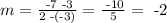
So, so far our equation looks like this
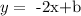
note that we want that this line passes through the point (2, -7). So this means that if we replace x by 2 then y is -7. So we have the equation
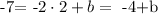
So if we add 4 on both sides we havethat
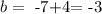
So our line equation would be
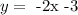
and the values of m and b are -2 and -3 respectively.