Question

Work: Gas mileage depends in part on the speed of the car. The gas mileage of asubcompact car is given, m(x) = -0.04x2 + 3.6x – 49, where 20 < x < 70 representsthe speed in miles per hour and m(x) is given in miles per gallon. WOHL EEN=--G:Given-List or Diagram the Data220Lx70m(x)= -0.047?_ 3,6x-49m(x) mpg>R: Required-what is the question?At what speed will the car get the maximum gas mileage?What is the maximum gas mileage?

Answer 1

We have to find at what speed will the car get the maximum mileage.

This can be done calculating the first derivative for m(x) in respect to x:

`\begin{gathered} m(x)=-0.04x^2+3.6x-49 \\ (dm)/(dx)=-0.04(2x)+3.6(1)-49(0)=-0.08x+3.6 \end{gathered}`

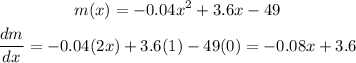
Now we equal it to 0 and solve for x:

`\begin{gathered} (dm)/(dx)=0 \\ -0.08x+3.6=0 \\ 3.6=0.08x \\ x=(3.6)/(0.08) \\ x=45 \end{gathered}`

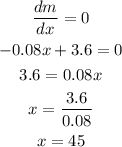
As x = 45 is within the valid interval (between 20 and 70), we know it is a valid solution.

The maximum mileage happens at 45 miles per hour.

We can now calculate this gas mileage as m(45):

`\begin{gathered} m(45)=-0.04(45)^2+3.6(45)-49 \\ m(45)=-0.04\cdot2025+162-49 \\ m(45)=-81+162-49 \\ m(45)=32 \end{gathered}`

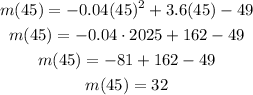
The maximum mileage is 32 miles per gallon.

We can see it in a graph as:

Answer: the maximum mileage happens at a speed of 45 miles per hour, and the maximum mileage is 32 miles per gallon.