Question

How do I solve this I am getting stuck help would be appreciated

Answer 1

Step-by-step explanation

Since this is a right triangle, we can compute the value of x by applying the trigonometric ratio, as shown as follows:

`\sin x=\frac{Opposite\text{ cathetus}}{\text{Hypotenuse}}=`

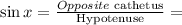
Plugging in the terms:

`\sin x=\frac{Opposite\text{ cathetus}}{\text{Hypotenuse}}=(7)/(9.4)`

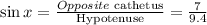
Computing the fraction:

`\sin x=(7)/(9.4)=(35)/(47)`

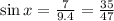
Applying sin^-1 to both sides:

`x=\sin ^(-1)((35)/(47))`

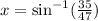
Computing the argument:

`x=48.131693\text{ degre}es`

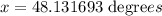
Rounding to the nearest tenth:

`x=48.1\text{ degre}es`

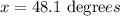
In conclusion, the value of x is 48.1 degrees