Question

Can anyone help me d. What is the probability that any randomly chosen pointwithin the square will be in the shaded area?e. What is the probability that the randomly chosen point willnot land in the shaded area?f. What is the probability that any point randomly selectedwithin the square will land on a specific point? On aspecific line?

Answer 1

Given:

Length of one side of the square = 12 units.

We have the following:

Area of the square = 12 x 12 = 144 square units

Area of the shaded region.

The shaded region forms a right triangle with the dimensions:

height = 8 units

Base = 11 units

The area will be:

`(1)/(2)*8*11=44\text{ square units}`

The area of the shaded region is 44 square units.

• Part d:

The probability that a randomly chosen point is in the shaded region.

To find the probability, apply the formula:

`\begin{gathered} P(shaded)\text{ = }\frac{Area\text{ of shaded region}}{Area\text{ of square}} \\ \\ =(44)/(144) \\ \\ =(11)/(36) \end{gathered}`

The probability that a randomly chosen point is in the shaded region is 11/36.

• Part e.

The probability that a randomly chosen point will not land in the shaded region.

To find the probability, apply the formula:

`\begin{gathered} P(not\text{ shaded\rparen = 1 - P\lparen shaded\rparen} \\ \\ =1-(11)/(36) \\ \\ =(36-11)/(36) \\ \\ =(25)/(36) \end{gathered}`

Therefore, probability that a randomly chosen point is not in the shaded region is 25/36.

• Part F.

What is the probability that any point randomly selected will land on a specific point.

The probability that any point randomly selected will land on a specific point will be:

`(1)/(144)`

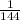
Now, the probability that any randomly selected point will land on a specific line will be:

`(1)/(144)`

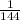
ANSWER:

• d. 11/36

,

• e. 25/36

,

• f. 1/144