Question

A police car waits in hiding slightly off the highway. A speeding car is spotted by the police car traveling at speed s = 34.8 m/s. At the instant the speeding car passes the police car, the police car accelerates forward from rest at a constant rate of a = 2.27 m/s2 to catch the speeding car. Assume the speeding car maintains its speed.Find the expression for the time that it takes for the police car to catch the speeding car

Answer 1

The speeding car moves at a constant speed v. The equation that describes the position of an object in uniform rectilinear motion is:

`x(t)=x_0+vt_{}`

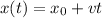
Where x₀ represents the initial position of the object at t=0.

Let the subindex 1 represent the speeding car. Let x=0 represent the position of the police car, and t=0 represent the time at which the speeding car passes by the police car. Then, the position of the speeding car at t=0 is 0. Then, we can use x_0=0 to describe the motion of the speeding car:

`x_1(t)=v_1t`

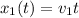
On the other hand, the police car is under constant acceleration. The equation that describes uniformly accelerated motion is:

`x(t)=x_0+v_0t+(1)/(2)at^2`

Where x₀ and v₀ represent the initial position and velocity of the moving object. Since the police car starts at rest, we can simplify this expression using x₀=0 and v₀=0. Let the subindex 2 represent the police car. Then:

`x_2(t)=(1)/(2)at^2`

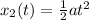
When the police car catches the speeding car, their positions are the same. Then:

`x_1(t)=x_2(t)`

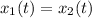
Substitute the expressions for the positions of the speeding car and the police car:

`v_1t=(1)/(2)at^2`

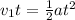
Divide both sides by t:

`\Rightarrow v_1=(1)/(2)at`

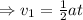
Isolate t from the equation:

`\Rightarrow t=(2v_1)/(a)`

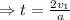
Substitute the values for the velocity of the speeding car and the acceleration of the police car to find the numerical value of the time that it takes for the police car to catch the speeding car:

`\begin{gathered} \Rightarrow t=(2(34.8(m)/(s)))/(2.27(m)/(s^2)) \\ =30.66079295\ldots s \\ \approx30.7s \end{gathered}`

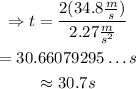
Therefore, the police car catches the speeding car approximately 30.7 seconds after they first meet.

If the speed of the speeding car is represented by the variable s, then the time that it takes for the police car to catch the speeding car is given by the expression:

`t=(2s)/(a)`

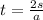
Where a represents the acceleration of the police car.