Question

Question 18Joaquin would like to prove that the following functions are inverses of each other using compositions.f(x) = 4x + 29(2) = 40 - 8What will the result be when he simplifiesf(g(x)) and9($(2))?А0B1СхD

Answer 1

The functions given are,

`\begin{gathered} f(x)=(1)/(4)x+2 \\ g(x)=4x-8 \end{gathered}`

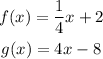
Firstly, Let us solve for f(g(x))

To resolve this, we will substitute x as 4x - 8 into the function f(x)

`\begin{gathered} f(g(x))=(1)/(4)(4x-8)+2 \\ f(g(x))=(1)/(4)*4x+(1)/(4)*-8+2 \end{gathered}`
`\begin{gathered} f(g(x))=x-2+2 \\ f(g(x))=x-0=x \\ \therefore f(g(x))=x \end{gathered}`

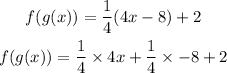
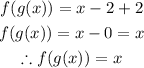
Let us now solve for g(f(x))

To resolve this, we will substitute x as 1/4x + 2 into the function g(x)

`\begin{gathered} g(f(x))=4((1)/(4)x+2)-8 \\ g(f(x))=4*(1)/(4)x+4*+2-8 \\ g(f(x))=x+8-8=x+0=x \\ \therefore g(f(x))=x \end{gathered}`

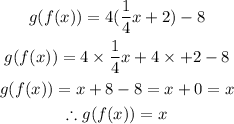
Therefore, the result will be

`x`