As the problem states, this is a piecewise function.
First, we will deal with the part of the function that is on the right side of the plane.
1. Right side
Notice that it is a line that is continuous towards the +x-direction.
The first thing we need to do is to calculate its domain (for which x's the function is defined).
That white dot means that the function is discontinuous in x=3, so, the domain of this section of the function is:
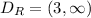
Now, notice that the lines correspond to the function:
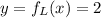
We will keep in mind these 2 results as we will use them to write the final form of the function.
2. Left side
Notice that there is a black dot (in contrast with the white dot on the right side), which means that the function is continuous in x=-3.
Once again, the first thing to do is to calculate the domain of the section of the function:
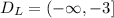
Then, notice that the line on the left side corresponds to the next function:
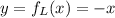
We can reach that result easily after noticing that the points (-3,3) and (-4,4) are in the line.
Summing up the results, we get the function that joins the left side and the right side:
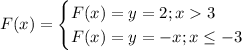
F(X) is the answer to the problem