Question

Calvin is graduating and wants to get a job in a government agency. He has done some research and will interview with two different agencies. The first agency offers starting yearly salaries with a mean of $47,000 and a standard deviation of $1,500. The second agency's average starting yearly salary is also $47,000, with a standard deviation of $4,000. With which agency is Calvin more likely tostart with an offer of $1,000 per week or more? Hint there are 52 weeks in a year.

Answer 1

Step-by-step explanation:

If Calvin starts with $1,000 per week or more, he will gain $52,000 per year or more, because:

52*$1000 = 52,000

Then, we need to standardize 52,000 with the mean and standard deviation of both agencies.

To standardize 52,000 we can use the following equation:

`\text{ z value =}\frac{52,000-mean}{\text{standard deviation}}`

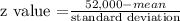
So, the z value for the first agency is:

`\text{ z-value=}(52,000-47,000)/(1,500)=3.33`

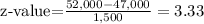
For the second agency:

`\text{ z-value=}(52,000-47,000)/(4,000)=1.25`

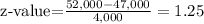
It is more probable to have a salary that is near to the mean, and the z-value gives us how far is the 52,000 from the mean.

Since the second agency has a smaller z-value, it is more likely to start with an offer of $1000 in the second agency.

Answer: The second agency