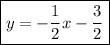Question

Find an equation for the line with the given properties. Express your answer using either the general form or the slope-intercept form of the equation of a line. slope=-1/2, contain the point (3,-3)

Answer 1

Step 1. We are given the slope of the line. We will call this slope 'm':

`m=-(1)/(2)`

We also have the point (3, -3) which we will label as (x1,y1):

`\begin{gathered} x_1=3 \\ y_1=-3 \end{gathered}`

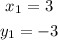
Required: Find the equation for the line.

Step 2. Since we have the slope and a point, we use the point-slope equation:

`y-y_1=m(x_-x_1)`

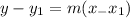
Substituting the known values:

`y-(-3)=-(1)/(2)(x-3)`

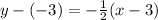
We will express our answer in the slope-intercept form:

`y=mx+b`

where m is the slope and b is the y-intercept.

Step 3. To convert our equation into the slope-intercept form, we need to simplify the operations:

`\begin{gathered} y-(-3)=-(1)/(2)(x-3) \\ \downarrow \\ y+3=-(1)/(2)x+(3)/(2) \end{gathered}`

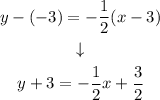
Subtract 3 from both sides:

`\begin{gathered} y=-(1)/(2)x+(3)/(2)-3 \\ \downarrow \\ \boxed{y=-(1)/(2)x-(3)/(2)} \end{gathered}`

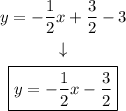
That is the equation in the slope-intercept form.

Answer:

`\boxed{y=-(1)/(2)x-(3)/(2)}`