Given:
Number of white counters = 10
Number of black counters = 6
Number of green counters = 4
Required: Probability
Explanation:
Total number of counters
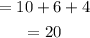
(a) Number of counters which are white or green
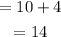
Probability of drawing a white counter or a green counter
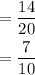
(b) Number of counters which are black or green
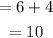
Probability of drawing a black counter or a green co