Question

Find the velocity at a time?Find the acceleration at time ?

Answer 1

ANSWERS

• v = 6cos(10) in/s ≈ 5.91 in/s

,

• a = -12sin(10) in/s² ≈ -2.08 in/s²

Step-by-step explanation

The velocity of an object is the derivative of its position with respect to time. Thus, to find the velocity of this object, we have to derive the function s(t) with respect to time,

`v(t)=(ds(t))/(dt)`

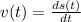
For this, we have to apply the chain rule. The inner function is u = 2t,

`v(t)=(ds(t))/(dt)=3\cdot(d(\sin(u)))/(du)\cdot(d(2t))/(dt)=3\cdot\cos (u)\cdot2`

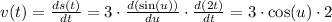
The velocity of the object is given by,

`v(t)=6\cos (2t)`

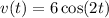
But we have to find the velocity at t = 5,

`v(5)=6\cos (2\cdot5)=6\cos (10)in/s\approx5.91in/s`

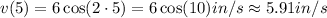
Hence, the velocity of the mass at t = 5 is 6cos(10) in/s

The acceleration of an object is the derivative of its velocity with respect to time,

`a(t)=(dv(t))/(dt)`

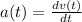
Again, we have to apply the chain rule with u = 2t,

`a(t)=(dv(t))/(dt)=6\cdot(d(\cos(u)))/(du)\cdot(d(2t))/(dt)=6\cdot(-\sin (u))\cdot2`

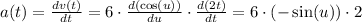
The acceleration of the object is given by,

`a(t)=-12\sin (2t)`

We also have to find the acceleration at t = 5,

`a(5)=-12\sin (2\cdot5)=-12\sin (10)in/s^2\approx-2.08in/s^2`

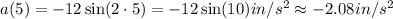
Hence, the acceleration of the mass at t = 5 is -12sin(10) in/s².