According to the given graph, a and b (that are the limits of the integral) are 1 and 3 respectively, this is because the area under the curve is being evaluated from 1 to 3.
It means that a=1 and b=3.
f(x) is the function of which we are calculating the integral. That function is a linear function. We can find it by finding the equation of the line:

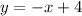
It means that f(x)=-x+4.
The area can be found using the definite integral:

It means that the area=4.