Question

11 m3 mNote: Where appropriate use either the pi button on your calculator or the approximation of"3.14". Round answers to the nearest tenth.Area of the base =Height =Volume =m3Blank 1:Blank 2:Blank 3:

Answer 1

The given diagram represents a right circular cylinder with radius of base (r) 3 meter, and height (h) 11 meter,

`\begin{gathered} r=3 \\ h=11 \end{gathered}`

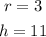
The base of the cylinder is a circle, so its area (A) is given by,

`A=\pi r^2`

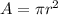
Substitute the value,

`\begin{gathered} A=\pi(3)^2 \\ A=\pi(9) \\ A\approx9*3.14 \\ A\approx28.3 \end{gathered}`

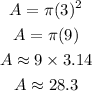
Thus, the area of the base is approximately 28.3 sq. meters.

Now, consider that the height is directly given as 11 meters.

So the Blank 2 would contain the value 11 meter.

The volume (V) of a right circular cylinder whose base area (A) and height (h) is known, is given by the formula,

`V=A\cdot h`

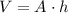
Substitute the values,

`\begin{gathered} V=28.26*11 \\ V=310.86 \\ V\approx310.9 \end{gathered}`

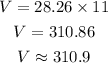
Thus, the volume of the given cylinder is approximately 310.9 cubic meters.

Therefore, the values in the three blanks are 28.3, 11, and 310.9, respectively.