Question

There exists a point D that is located on AB and is one-third of the way from C to B.

Answer 1

(5, 4)

Step-by-step explanation

We are given that C is the midpoint from A to B.

First, we have to find the coordinates of point C.

To do that, we apply the formula for midpoint of two points:

`C=((x_2+x_1)/(2),(y_2+y_1)/(2))`

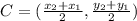
where (x1, y1) and (x2, y2) are the two points.

The coordinates of A and B are (-3, 8) and (9, 2)

Therefore, the coordinate of C is:

`\begin{gathered} C=((-3+9)/(2),(8+2)/(2)) \\ C=((6)/(2),(10)/(2)) \\ C=(3,5) \end{gathered}`

Point D is given to be one-third the distance between C and B.

This means that we want to partition the distance between C and B into 3, where D is the point 1/3 that distance away from C.

To find D, we have to find the difference between the coordinate points of C and B, find 1/3 of that, then, add that to the coordinate of C:

`\begin{gathered} (1)/(3)(9-3,2-5)=((1)/(3)\cdot6,(1)/(3)\cdot-3) \\ (2,-1) \end{gathered}`

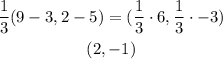
Adding that to the coordinates of C:

`\begin{gathered} D=(3+2,5+(-1))=(3+2,5-1) \\ D=(5,4) \end{gathered}`

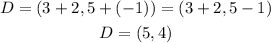
That is the coordinate of D.