Question

1. A poll conducted in 2018 found that 54% of US adult Twitter users get at least some news on Twitter. The standard error for this estimate was 2.4%, and a normal distribution can be used to model the sample proportion. Construct a 99% confidence interval for the fraction of US adult Twitter users who get some news on Twitter, and interpret the confidence interval in context.

Answer 1

The 99% confidence interval for the fraction of US adult Twitter users who get some news on Twitter is (0.4872, 0.6018). It means that we are 99% sure that the true proportion of US adult Twitter users who get some news on Twitter is between 0.4872 and 0.6018.

Explanation:

In a sample with a number n of people surveyed with a probability of a success of
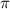`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm zs`

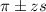
In which

z is the zscore that has a pvalue of
`1 - (\alpha)/(2)`, and s is the standard error.

54% of US adult Twitter users get at least some news on Twitter.

This means that
`\pi = 0.54`

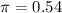
The standard error for this estimate was 2.4%

This means that
`s = 0.024`

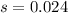
99% confidence level

So
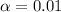`\alpha = 0.01`, z is the value of Z that has a pvalue of
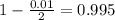`1 - (0.01)/(2) = 0.995`, so
`Z = 2.575`

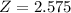
The lower bound is:

`\pi - zs = 0.54 - 2.575*0.024 = 0.4782`

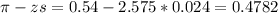
The upper bound is:

`\pi + zs = 0.54 + 2.575*0.024 = 0.6018`

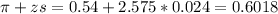
The 99% confidence interval for the fraction of US adult Twitter users who get some news on Twitter is (0.4872, 0.6018). It means that we are 99% sure that the true proportion of US adult Twitter users who get some news on Twitter is between 0.4872 and 0.6018.