1 Answer

Donghua Liu · Answer 1 · 2023-10-13T22:02:15+0000

We are asked to determine the volume of a sphere. To do that we will use the following formula:

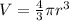
$V=(4)/(3)\pi r^3$

Where "r" is the radius.

We are given that the diameter is 8cm. We have that:

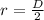
Where "D" is the diameter. This means that the radius is half the diameter. Substituting we get:

$r=\frac{8\operatorname{cm}}{2}=4\operatorname{cm}$

Now we substitute in the formula for the volume:

$V=(4)/(3)\pi(4\operatorname{cm})^3$

we will use:

$\pi=3$

Substituting we get:

$V=(4)/(3)(3)(4\operatorname{cm})^3$

Now we solve the operations:-

$V=4(4\operatorname{cm})^3=256\operatorname{cm}^3$

Therefore, the volume of the sphere is 256 cubic centimeters.

Please log in or register to add a comment.