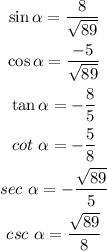Question

An angle A standard position has a terminal side which passes through (-5,8) Determine values of the following sin Acos Atan A cot Asec Acsc A

Answer 1

If the point in the angle's terminal side is P = (x,y) then the trigonometric functions can be calculated as:

sin α = y/r

cos α = x/r

tan α = y/x

cot α = x/y

sec α = r/x

csc α = r/y

Where r is

`√(x^2+y^2)`

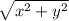
For the given point we have:

`r=√((-5)^2+(8)^2)=√(25+64)=√(89)`

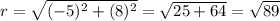
So the functions are:

Answer

`\begin{gathered} \sin\alpha=(8)/(√(89)) \\ \cos\alpha=(-5)/(√(89)) \\ \tan\alpha=-(8)/(5) \\ cot\text{ }\alpha=-(5)/(8) \\ sec\text{ }\alpha=-(√(89))/(5) \\ csc\text{ }\alpha=(√(89))/(8) \end{gathered}`