Question

What is a solution to the system of equations that includes quadratic function f(x) and linear function g(x)?f(x) = 5x2 + x + 3A. (-1, 7)B. (0, 3)C. (0, 7) D. (1, 9)

Answer 1

(1, 9)

Explanation:

I got it right on the test.

Answer 2

In order to find the solution of the system of equations, we need to find the equation for function g(x). By taking 2 consecutive row of the table, the slope is given by

`m=(5-3)/(-1-(-2))=(2)/(1)=2`

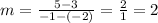
and from the given table, we can note that the y-intercept (b) is 7 because at x=0, g(0)=7. Then, the equation of g(x) is

`g(x)=2x+7`

So, the equations will have a common solution when

`f(x)=g(x)`

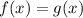
which implies

`5x^2+x+3=2x+7`

By moving 2x +7 to the left hand side, we obtain

`5x^2-x-4=0`

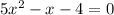
By applying the quadratic formula,

`x=(-b\pm√(b^2-4ac))/(2a)`

with a=5, b=-1 and c=-4, we get

`x=(1\pm√(1^2-4(5)(-4)))/(10)`

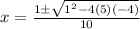
which gives

`x=(1\pm√(81))/(10)=(1\pm9)/(10)`

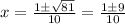
Then, one solution is x=1 and a second solution is x=-0.8.

If we insert our first solution into g(x), we get

`g(1)=2(1)+7=9`

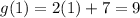
So, one solution of our system or equation is (1,9). Therefore, the answer is the last option (1,9)