Answer:
1. The sequence is an arithmetic sequence since there's a common difference of 200 between the terms of the sequence.
2. The sequence is a geometric sequence since there's a common ratio of 4 between the terms of the sequence
Step-by-step explanation:
In an arithmetic sequence, there will be a common difference(d) between the terms of the sequence.
While in a geometric sequence, there will be a common ratio between the terms of the sequence.
1) Given the below sequence;
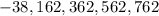
Let's determine if the sequence above is an arithmetic or geometric sequence;
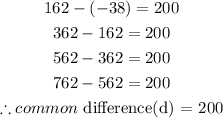
Since there's a common difference of 200 between the terms of the sequence, therefore, we can say that the sequence is an arithmetic sequence.
2) Given the below sequence;

Let's determine if the sequence above is an arithmetic or geometric sequence;
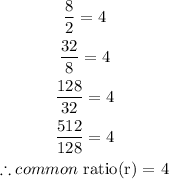
Since there's a common ratio of 4 between the terms of the sequence, therefore, we can say that the sequence is a geometric sequence.